运筹研究assignment-关键概念

问题1.解释运筹学模型的类型。简要解释运筹学的阶段？

Q.1 Explain the types of Operations Research Models. Briefly explain the phases of Operations Research?

 

Ans 回答

运筹学：运用科学的方法、技术和工具，对一个系统进行操作，使问题得到最佳的解决方案，而最佳化则指最佳方案.。

研究模型的类型：

物理模型：-有两种类型-标志性和模拟模型。这些模型包括图表、图表和图表的所有形式.。他们是设计来解决具体问题。他们提出了重要的因素和相互关系的图片形式，便于分析。

 

Operation Research : The application of scientific method ,techniques and tools to the operation of a system with optimum solution to the problem and where optimum refers to the best possible alternative .

 

Types of research model:

 

Physical model:- There are two types -iconic and analog model. Theses models include all form of diagrams, graphs, and charts. They are design to tackle specific problems. They bring out significant factors and interrelationship in pictorial form to facilitates analysis.

 

Mathematical or symbolic Model: - These models employ a set of mathematical symbol to represent the decision variable of the system. The variables are related by mathematical systems. Some examples of mathematical model are allocation, sequencing and replacement models.

 

Models by nature of environment: - Two types of it Deterministic and probabilistic models.

 

Deterministic Model – These are the models in which everything is defined and the results are certain, such as EOQ model.

Probabilistic Model – There are the model in which the input and output variables follow a defined probability distribution, such as the games theory.

Models by extent of generality:-

 

General models – These are the models which can apply in general to any problem. For example- linear programming.

Specific model - These are the model that you can apply only under specific condition. For example, you can use the sales response curve or equation as a function in marketing function.

Phases of Operational research –

 

Judgement Phase –

Determination of the operations.

Establishment of objectives and values related to the operations.

Determination of suitable measures of effectiveness.

Formulation of problems relative to their objective.

Research phase -

Operation and data collection for a better understanding of the problems

Formulation of hypothesis and model.

Observation and experimentation to test the hypothesis on the basis of additional data.#p#分页标题#e#

Analysis of the available information and verification of the hypothesis using pre-established measure of effectiveness.

Action Phase –

The phase involves making recommendations for the decision process. The recommendation can be made by those who identify and present the problem or by anyone who influences the operation in which the problem has occurred.

Q. 2 a. Explain the graphical method of solving Linear Programming Problem.

 

b. A paper mill produces two grades of paper viz., X and Y. Because of raw material restrictions, it cannot produce more than 400 tons of grade X paper and 300 tons of grade Y paper in a week. There are 160 production hours in a week. It requires 0.20 and 0.40 hours to produce a ton of grade X and Y papers. The mill earns a profit of Rs. 200 and Rs. 500 per ton of grade X and Y paper respectively. Formulate this as a Linear Programming Problem. ?

 

Ans Linear Program Problem - is a mathematical technique design to help managers in their planning and decision –making .It is usually used in an organisation that is trying to make the most effective use of its resources . Resoucrces typically include machinery , manpower , money, time , warehouse space and raw materials .

 

For obtaining an optimal solution to an LPP by graphical method, the statement of following theorems of linear programming is used:

The collection of all feasible solution to an LPP constitutes a coves set whose extreme points corresponds to the basic feasible solution.

There are finite number of basic feasible regions within the feasible solution space.

If the cnvex set of the feasible solution of the system of simultaneous equation is a covex polyhedron, than atleast one of the extreme points gives an optimal solution.

If the optimal solution occurs at more than one extreme point, the value of objective function will be the same for all convex combination of these extreme points

Formulation: Maximize: 200x + 500y Subject to: x<= 400 y<= 300 2x + 4y <= 1600 Solution: x = 200 tons y = 300 tons Profit = 190000

Q.3 a. Explain how to solve the degeneracy in transportation problems.

 

b. Explain the procedure of MODI method of finding solution through optimality test ?

 

Ans - Degeneracy in transportation problem –

 

A basic solution to an m- origin , n destination transportation problem can have the most m+ n-1 positive basic variable (non-zero) , otherwise the basic solution degenerates . It follows that whenever the number of basic cells is less than m+n-1, the transportation problem is degenerate one .

 

Degeneracy develops in two ways –

 

It develops while determining an initial assignment via anyone of the initial assignment methods discussed earlier .#p#分页标题#e#

It develops at the iteration stage . This happens when the selection of entering variables results in simultaneous drive to zero of two or more current ( pre-iteration) basic variables .

(MODI METHOD) – Transportation Algorithms

 

A feasible solution has to be found always. Rather than determining a first approximation by a direct application of the simplex method, it is more efficient to the work with the transportation table . The transportation algorithm is the simplex method specialised to the format of the table involving the following steps:-

 

Finding an initial basic feasible solution.

Testing the solution for optimality.

Improving the solution , when it is not optimal

Repeating steps (i) and (iii) until the optimal solution is obtained.

Solution to the transportation problem is obtained in 2 stages-

 

In first stage we find the basic feasible solution using any of the following method –

North – west corner rule.

Matrix minima method or least cost method.

Vogel’s approximation method.

In second stage, we test the babis feasible solution for the optimality by MODI METHOD.

Q.4 a. Explain the steps involved in Hungarian method of solving Assignment problems.

 

b. What do you mean by unbalanced assignment problem? How do you overcome it?

 

Ans

 

Hungarian Method Algorithm:- is based on the concept of opportunity cost and is more efficient in solving assignment problem.

 

Steps to solve the problem are as follows-

 

Prepare row ruled matrix by selecting the minimum values for eah row and subtract it from the other elements of the row .

Prepare column-reduced matrix by subtracting minimum value of the column from the other values of the column.

Assign zero row-wise if there is only one zero in the row and cross(X) or cancel other zeros in that column.

Assign column wise if there is only one zero in that column and cross other zeros in that row.

Repeat steps 3 and 4 till all zero are either assigned or crossed. If the number of assignments is equal to the number of row present, you have arrived at an optimal solution, if not , proceed to step 6 .

Mark (√) the unassigned row. Look for crossed zero in that row. Mark the column containing the crossed zero .Look the assigned zero in that column. Mark the row containing the assigned zero .Repeat this process till all the markings are done.

Draw a straight line through unmarked rows and marked column. The number of straight line drawn will be equal to the assignment made.

Examine the uncovered elements. Select minimum.#p#分页标题#e#

Subtract it from the uncovered elements.

 

Add it at the point of intersection of lines.

 

Leave the rest as is

 

Prepare a new table.

 

Repeat steps 3 to 7 till optimum assignment is obtained.

Repeat step 5 to 7 till number of allocation= number of rows.

Unbalanced Assignment Problem:- where the number of the rows is not equal to the number of columns and vice versa . For example – the number of machines may be more than the number of jobs or the number of jobs may be more than the number of machines. In such a situation, you have to introduce dummy rows or column in the matrix. The dummy row column will contain all cost elements as zero. This balances the program and then we can use Hungarian method to find the optimal assignment.

 

Unbalnced assignment problem: No. Of rows ≠ NO. Of columns.

 

Q.5

 

a. Write a short note on Monte Carlo Simulation.

 

b. A Company produces 150 cars. But the production rate varies with the distribution.

 

At present the track will hold 150 cars. Using the following random numbers determine the average number of cars waiting for shipment in the company and average number of empty space in the truck. Random Numbers 82, 54, 50, 96, 85, 34, 30, 02, 64, 47?

 

Ans :-

 

A)Monti Carlo simulation is a simulation technique in which statistical distribution function are created by using a series of random numbers . This approach has the ability to develop many months or years of data in a matter of few minutes on a digital computer. This method is generally used to solve the problems that cannot be adequately represented by mathematical models or where solution of the model is not possible by analytical method.

 

B)

 

Solution:

 

 

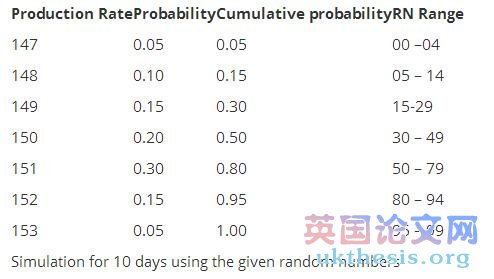
Therefore, Avg number of cars waiting =8/10= 0.8 /day

 

Avg number of empty space =3/10= 0.3/day

 

Q.6 a. Explain the dominance principle in game theory.

 

b. Describe the Constituents of a Queuing System.

 

c. Differentiate between PERT and CPM. ?

 

Ans

 

a. Dominance principle in game theory:- In a rectangular game ,

 

- In the pay-off matrix, if each pay-off in Rth row is greater than( or equal) the corresponding pay-off in the sth row, Ar dominates As .#p#分页标题#e#

 

- In the pay-off matrix,if each pay-off in pth column is less than (or equal to ) the corresponding pay-off in the qth column , Bp dominates Bq .

 

b. Constituents of a Queuing System:- It includes

 

Arrival Pattern- It is the average rate at which the customers arrive.

Service Facility- Examining the number of customers served at a time and the statistical pattern of time taken for the service at the service facility.

Quene Facility - The common method of choosing a customer for service amongst those waiting for service is ‘First Come First serve’.

c. Difference between PERT and CPM.

 

PERT

 

It was developed in connection with an Research and Development work.

It is an event- oriented network as in the analysis of a network, emphasis is given on the important stages of completion of a task rather than the activities required to be performed to reach a particular event or task.

PERT is normally used for projects involving activities of non-repetitive nature in which time estimates are uncertain.

It helps in pinpointing critical areas in a project, so necessary adjustment can be made to meet the scheduled completion date of the project.

CPM

 

It was developed in connection with a construction project, which consisted of routine tasks whose resources requirement and duration were known with certainty, Therefore it is basically deterministic.

It is suitable for establishing a trade-off for optimum balancing between schedule time and cost of the project.

It used for projects involving activities of repetitive nature.